源码版本:PG13
Free Space Map 是 PostgreSQL 空闲空间高效管理的一种方式。堆表由于频繁的 update, delete,vacuum,会导致页面出现大小不一的空闲空间,FSM 机制能够有效的管理这些空闲空间,当需要一块指定大小的空闲空间时,通过 FSM 机制可以快速查找到。
1. FSM 原理
FSM 使用 1 个字节存储一个堆表页面内的空闲空间,1 个字节可以表示 0~255 共 256 种状态,将一个 page 的大小除以 256,就能得到 256 个档位,称之为 cat 值,使用 1 个字节来表示这 256 个档位,其对应关系如下:
Category Range
0 0~31
1 32~63
... ...
255 8164~8192
举个例子,假设 1 字节的值为 255,则表示其对应的 page 页面至少有 8164 个字节的空闲空间。这种方式与 clog 使用 2 bit 表示事务状态类似, 但是这种方式有一个致命缺点,就是查找满足指定大小的空间效率低下,需要遍历所有 FSM 页面,直到找到一个满足指定大小的空闲空间。
2. 大根堆二叉树
为了解决查找指定大小空闲空间效率低下的问题,FSM 引入了大根堆二叉树的数据结构,即该二叉树的根节点是所有子节点的最大值。叶子节点存储的是实际 heap 表的空间值(cat值),非叶子节点为辅助结构,用于快速查找。大根堆二叉树如下:
4
4 2
3 4 0 2
一个 FSM 页面由两部分组成,叶子节点和非叶子节点。由二叉树的原理可知,二叉树的叶子节点与非叶子节点的比例,大约为1:1,即一个 FSM 页面前一半为非叶子节点,后一半为叶子节点,该页面本身即为一个局部的二叉树,有利于快速查询页面内部的叶子节点。
PG 源码中相关的宏定义:
一个 fsm page 能够包含的 node 数量:
#define NodesPerPage (BLCKSZ - MAXALIGN(SizeOfPageHeaderData) - \
offsetof(FSMPageData, fp_nodes))
一个 fsm page 非叶子节点的数量:
#define NonLeafNodesPerPage (BLCKSZ / 2 - 1)
一个 fsm page 叶子节点的数量:
#define LeafNodesPerPage (NodesPerPage - NonLeafNodesPerPage)
PG 的最大页面数量约为 2^32,3 层二叉树能够表示的最大页面数约为 LeafNodesPerPage^3,默认 8KB 的页面大小,LeafNodesPerPage^3 远大于 2^32,因此 FSM 的二叉树最多 3 层即能满足 PG 的最大页面映射需求。
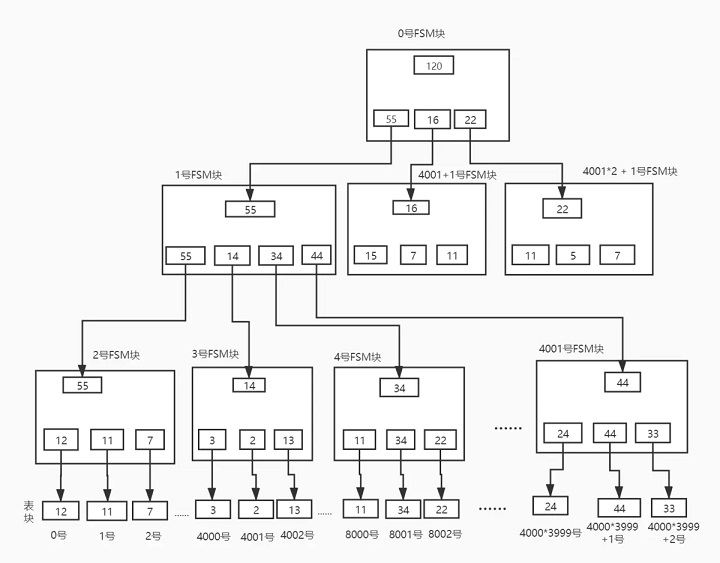
FSM 文件内所包含的 FSM 页面和 heap 页面的映射关系如下图所示:
-
第 3 层为叶子节点,其从 FSM 的 page 2 开始,页面连续,最多有 LeafNodesPerPage^2 个页面,页面的前半部分为页内局部二叉树的非叶子节点,后半部分为叶子节点,可以将其看作为数组,其 index 表示 heap 表的 page 号,值表示 heap 表的 page 号对应的空闲 cat 值。
-
第 2 层为非叶子节点,其从 FSM 的 page 1 开始,其页面不连续,最多有 LeafNodesPerPage 个页面,页面的前半部分为页内局部二叉树的非叶子节点,后半部分为叶子节点,表示第3层的节点空闲值。可以将其看作为数组,其 index 表示第 3 层节点的 page 号,值表示第 3 层节点的 page 号对应的空闲 cat 值。
-
第 1 层为根节点,其位于 FSM 的 page 0 ,只占用一个页面。页面的前半部分为页内局部二叉树的非叶子节点,后半部分为叶子节点,表示第2层的节点空闲值。可以将其看作为数组,其 index 表示第 2 层节点的 page 号,值表示第 2 层节点的 page 号对应的空闲 cat 值。
每个 FSM 页面的局部二叉树的根节点存储了当前页面表示的最大空闲 cat 值,因此寻找一个满足指定大小的 heap 页面,只需从 FSM 的根节点查找二叉树即可,效率非常高。
为了避免高并发下每个 backend 进程每次都从 FSM page 0 的根节点进行查找,FSM 页面设置了 fp_next_slot 值,提示下一次开始查询二叉树时的叶子节点位置,这样能够避免根节点成为热点。
3. 源码实现
树状结构使用 FSMAddress 结构体表示。
typedef struct
{
int level; /* level */
int logpageno; /* page number within the level */
} FSMAddress;
level 表示树节点的层级,其中 0 表示叶子节点,FSM_TREE_DEPTH 表示树深度,根据页面的大小,通常为 3 或 4 层,默认 8KB 页面下为 3 层。
函数 fsm_logical_to_physical() 能够把 FSMAddress 表示的树状节点逻辑页号转换成物理页号,即逻辑页号与物理页号之间有一个对应关系。
获取父节点:
static FSMAddress
fsm_get_parent(FSMAddress child, uint16 *slot);
获取子节点:
static FSMAddress
fsm_get_child(FSMAddress parent, uint16 slot)
4. 查找一个指定 heap 页的剩余空间
(1)调用 pg_freespacemap 插件中的 pg_freespace() 函数,参数为表的 relid 和 blkno
(2)调用 GetRecordedFreeSpace(relid, blkno) 函数
(3)根据 blkno 获取其对应的 FSMAddress 地址 addr 以及 slot,转换规则如下:
addr.level = FSM_BOTTOM_LEVEL;
addr.logpageno = heapblk / SlotsPerFSMPage;
*slot = heapblk % SlotsPerFSMPage;
(4)根据 addr 获取其对应的 fsm 物理页面 buf,主要通过 fsm_logical_to_physical() 函数进行转换。
(5)有了 buf 和 slot,就能获取 heap 页对应的 cat 值,如下:
FSMPage fsmpage = (FSMPage) PageGetContents(buf);
return fsmpage->fp_nodes[NonLeafNodesPerPage + slot];
(6)有了 cat 值,通过 fsm_space_cat_to_avail() 得到空闲空间大小,如下:
if (cat == 255)
return MaxFSMRequestSize;
else
return cat * FSM_CAT_STEP;
5. 查找一个指定大小的空闲空间
(1)调用 GetPageWithFreeSpace() 函数,参数为 rel 和 spaceNeeded
(2)调用 fsm_space_needed_to_cat() 函数,将 spaceNeeded 转换为最小的 min_cat 值
(3)调用 fsm_search() 函数,参数为 rel 和 min_cat。函数内部从搜索二叉树根节点 FSM_ROOT_ADDRESS 开始,在一个大循环内,首先找到大于 min_cat 的节点,如果其 level 不是叶子节点,则进入到它的子节点中继续查找,直到找到值大于 min_cat 并且 level 是叶子节点为止。
参考资料:
文章评论